When we solved the system in which a particle is confined to an infinite box (that is, an infinite square well), we saw that quantum numbers arose naturally through the enforcement of continuity conditions (that th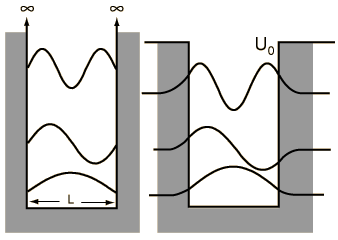 e wavefunction ψ must go to zero at x=0 and x=L). Quantization of energy and position (namely, nodes at which the particle cannot exist) are directly to these quantum numbers, whose values are n=1, 2, ..., ∞, representing an infinite number of energy levels.
e wavefunction ψ must go to zero at x=0 and x=L). Quantization of energy and position (namely, nodes at which the particle cannot exist) are directly to these quantum numbers, whose values are n=1, 2, ..., ∞, representing an infinite number of energy levels.
 e wavefunction ψ must go to zero at x=0 and x=L). Quantization of energy and position (namely, nodes at which the particle cannot exist) are directly to these quantum numbers, whose values are n=1, 2, ..., ∞, representing an infinite number of energy levels.
e wavefunction ψ must go to zero at x=0 and x=L). Quantization of energy and position (namely, nodes at which the particle cannot exist) are directly to these quantum numbers, whose values are n=1, 2, ..., ∞, representing an infinite number of energy levels.A particle in a finite box, however, can tunnel into the walls, in the same fashion that we saw earlier with the two barrier problems. Solving this system is not difficult but, unfortunately, has no analytical solution and must be solved either numerically or, as was done in class, graphically. On the other hand, the wavefunctions are essentially just those from the infinite box but are allowed to bleed into the wall (with the caveat that higher energy states tunnel further than the lower energy states). To summarize the major differences between the particle in a finite box and one in an infinite box:
- only a finite number of energy levels exist [called bound states]
- tunneling into the barrier is possible
- higher energy states are less tightly bound than lower states
- a particle given enough energy can break free [in other words, unbound]
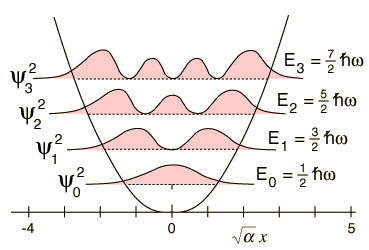
One important distinction from the particle in a box result is that the peaks in the wavefunction are not uniform. For example, for v=2 and larger, it is clear that outside peaks (representing larger displacement from x=0) have higher probability than inside peaks. As n gets large, we see another clear example of the correspondence principle.

14 comments:
Could you put up the solutions to HW 3 please.....
I was hoping you could post the exam 1 topic sheet this weekend!!
Thanks,
Amanda
the HW 3 solutions posted are actually HW 1. If you could change it that would be great...
For Hw 3, the question for 7a varies between the actual hw question and the solutions.
true, but that shouldn't be a problem.
maybe i should claim that i intentionally do that to keep students on their toes?
That would certainly do the trick. While you're at it, care to explain mathematically to me how 0!=1?
Yes, it does seem weird that 0! = 1 but check this out:
Clearly n! = (n -1)! x n
Rearranging, we get:
(n - 1)! = n!/n
Setting n = 1 gives you that 0! = 1
Another way to impress your friends and family.
Just don't put n=0 in there cause that will make the world blow up.
Using n=0 would be devastating to the mind, as can be seen by my current state. If (n - 1)! = n!/n is true, then how can the result of -1!=-1? For surely you would have to use n=0
You're not going to like this but -1! is actually complex_infinity. Yes, not just ordinary_infinity, but complex_infinity. Have fun with that.
For problem 05 on HW 03, does Xtp represent the turning point between classical physics and QM when looking at kinetic energy?
I guess I'm just confused by the math when calculating Xtp in part (a) and all the different substitutions
any help or clarification maybe?
Yay, I love it when people use the blog...
The turning point is purely classical and is often called "the classical turning point". As mentioned in lecture, it is that point at which a harmonic oscillator (whether a pendulum or a spring) will stop and turn the other direction. From classical physics, that is the instant at which the system runs out of kinetic energy and all energy is potential.
A quantum oscillator has no deterministic turning point (and is, rather, entirely probabilistic) so we should interpret the term only as an analogy to classical mechanics.
We often refer to classical analogs, as you may have noticed in lecture, because quantum mechanics obeys physical laws that are utterly un-visualizable. Although quantum mechanics is the ultimate law of the universe, we have fleeting experience with it since we, as macroscopic entities, only experience average quantities (which are, in fact, averages over unimaginable numbers of particles).
привет красивый мужчина. когда будш Tы, чтобы посетить нас в Киеве?
Who knows where to download XRumer 5.0 Palladium?
Help, please. All recommend this program to effectively advertise on the Internet, this is the best program!
Alguien me podría decir cuáles son las principales diferencias entre la aproximación de la partícula en una caja unidimensional y la aproximación del oscilador armónico cuántico? Como afectan nuestra concepción de la naturaleza?
Post a Comment