PreExam MerryGoRound O Questions 2

Fire away, again.

PreExam MerryGoRound O Questions

Fire away...

Rigid Rotation in 2d and 3d

After having studied translation and vibration in the particle-in-a-box and harmonic oscillator quantum systems, respectively, it is natural to turn to rotation. The simplest such system is the particle on a ring (also called rigid rotation in 2d) which, after replacing the mass m with the reduced mass μ can be used for two-body problems (like a diatomic molecule).

Since the potential is a constant we can define it to be zero. The natural coordinate system to use is polar coordinates which greatly simplifies the Schrödinger Equation:

(-hbar²/2I) ∂²/∂φ²ψ = Eψ

This is identical to the very first problem we solved, expect we have traded translational properties (x, m) with rotational analogs (φ, I), a standard practice seen even in classical physics. This leads to, after normalizing, the following equation:

ψ(φ) = 1/√2π e^imφ

Continuity conditions demands that cyclic boundary conditions hold; that is, that ψ(φ + 2π) = ψ(φ). This restriction leads directly to quantization, and the quantum number m_l can only take integral values. This restriction on m_l requires that both energy and position/displacement be quantized.

Further, after constructing the appropriate operator, we see that we have a new quantized property arises naturally in angular momentum, called L_z because the vector lies perpendicular to the plane of rotation.

Rotation in 3d is very similar but we need to use spherical coordinates...

Success

Success in physical chemistry requires a student to do more than just work homework problems (or, in some cases, just looking at the solutions to the homework problems). A knowledge of the fundamental concepts that are threaded throughout the study of quantum systems are absolutely essential to pass this class (for example, multiplicative wavefunctions that lead to additive energies as part of the method of separation of variables). Perhaps what is needed is less of a focus on, say, what might appear on the equation sheet and more on the basic tenets of quantum mechanics.

RS

Particle in a Finite Box and the Harmonic Oscillator

When we solved the system in which a particle is confined to an infinite box (that is, an infinite square well), we saw that quantum numbers arose naturally through the enforcement of continuity conditions (that th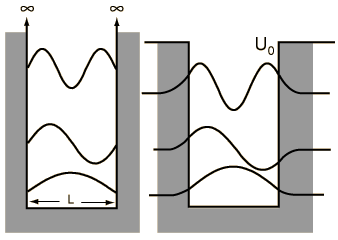e wavefunction ψ must go to zero at x=0 and x=L). Quantization of energy and position (namely, nodes at which the particle cannot exist) are directly to these quantum numbers, whose values are n=1, 2, ..., ∞, representing an infinite number of energy levels.

A particle in a finite box, however, can tunnel into the walls, in the same fashion that we saw earlier with the two barrier problems. Solving this system is not difficult but, unfortunately, has no analytical solution and must be solved either numerically or, as was done in class, graphically. On the other hand, the wavefunctions are essentially just those from the infinite box but are allowed to bleed into the wall (with the caveat that higher energy states tunnel further than the lower energy states). To summarize the major differences between the particle in a finite box and one in an infinite box:

• only a finite number of energy levels exist [called bound states]
  
• tunneling into the barrier is possible
  
• higher energy states are less tightly bound than lower states
• a particle given enough energy can break free [in other words, unbound]

The next quantum system to investigate is the one-dimensional harmonic oscillator, whose potential [from Hooke's Law] is V=1/2kx². Plugging this into the Schrödinger Equation leads to, after some well-chosen substitutions, a differential equation solved by Hermite in the mid-1800's, and we obtain the wavefunction: ψ(x) = N_vH_ve^-q2/2, where q = αx, v is the quantum number [v=0, 1, ...] and H_v are the Hermite polynomials. Here we see energy quantization as well, giving E = (v + 1/2)hbarω. This quantum system is the only one to exhibit constant spacing but other results mirror those seen in prior examples: tunneling into classically forbidden zones (where x represents displacement from equilibrium rather than position), a nonzero ground state energy as well as the existence of nodes.

One important distinction from the particle in a box result is that the peaks in the wavefunction are not uniform. For example, for v=2 and larger, it is clear that outside peaks (representing larger displacement from x=0) have higher probability than inside peaks. As n gets large, we see another clear example of the correspondence principle.

Obits

Wow, first John Wheeler on Sunday and today Edward Lorenz. A sad week for science...

Finite Barrier Tunneling and the Uncertainty Principle

When a quantum particle encounters a discontinuity in the form of a finite barrier, there is a nonzero probability that it will be transmitted to the other side of the barrier. In fact, as the graphic at right shows, the wavefunction bifurcates into a reflected as well as a transmitted part, a decidedly nonclassical and headscratching result (remember the Copenhagen interpretation) -- the three curves, by the way, show the real and imaginary parts of the wavefunction as well as the probability density.

Such tunneling phenomena are found throughout physics, chemistry and molecular biology, from explanations of alpha and beta decay to kinetic isotope effects and electron and proton transport in enzymes. It is likely that all redox chemistry has a tunneling component, which becomes even more prominent as the temperature falls.

Before moving onto the next quantum system, the particle in a finite box, we take a moment to consider one of the most important discoveries in all of quantum mechanics, the uncertainty principle. Heisenberg, in his development of matrix mechanics (an alternate description of quantum behavior, using matrices instead of differential operators), he discovered that some matrices did not commute, particularly those for momentum and position. After a little work he was able to demonstrate that this placed limits on the knowledge of the corresponding observable and we were doomed to indeterminacy. In particular, he found that ∆x∆p ≥ hbar/2, where ∆x and ∆p are the standard deviations of position and momentum.

Classically these values are zero: we can always know the position of, say, a marble and its velocity (and hence its momentum). At the quantum scale, these values are nonzero and, more baffling, are connected. The more precise we can nail down the position, for example, the less we will know about its momentum (and vice versa). Clearly we have to give up the Newtonian idea of knowing the trajectory of any quantum particle. This is not really an issue with measurement itself but rather a fundamental description of the quantum nature of the universe.

As we will see there are a number of uncertainty principles and they arise whenever we have noncommutative operators. In other words, whenever [a,b] ≠ 0, we will have an uncertainty principle in the corresponding observables: ∆a∆b ≥ hbar/2.