Wednesday, April 30, 2008
Tuesday, April 29, 2008
Rigid Rotation in 2d and 3d
After having studied translation and vibration in the particle-in-a-box and harmonic oscillator quantum systems, respectively, it is natural to turn to rotation. The simplest such system is the particle on a ring (also called rigid rotation in 2d) which, after replacing the mass m with the reduced mass μ can be used for two-body problems (like a diatomic molecule).
Since the potential is a constant we can define it to be zero. The natural coordinate system to use is polar coordinates which greatly simplifies the Schrödinger Equation:
This is identical to the very first problem we solved, expect we have traded translational properties (x, m) with rotational analogs (φ, I), a standard practice seen even in classical physics. This leads to, after normalizing, the following equation:
Further, after constructing the appropriate operator, we see that we have a new quantized property arises naturally in angular momentum, called Lz because the vector lies perpendicular to the plane of rotation.
Rotation in 3d is very similar but we need to use spherical coordinates...
Since the potential is a constant we can define it to be zero. The natural coordinate system to use is polar coordinates which greatly simplifies the Schrödinger Equation:
(-hbar2/2I) ∂2/∂φ2ψ = Eψ
This is identical to the very first problem we solved, expect we have traded translational properties (x, m) with rotational analogs (φ, I), a standard practice seen even in classical physics. This leads to, after normalizing, the following equation:
ψ(φ) = 1/√2π eimφ
Further, after constructing the appropriate operator, we see that we have a new quantized property arises naturally in angular momentum, called Lz because the vector lies perpendicular to the plane of rotation.
Rotation in 3d is very similar but we need to use spherical coordinates...
Monday, April 28, 2008
Success
Success in physical chemistry requires a student to do more than just work homework problems (or, in some cases, just looking at the solutions to the homework problems). A knowledge of the fundamental concepts that are threaded throughout the study of quantum systems are absolutely essential to pass this class (for example, multiplicative wavefunctions that lead to additive energies as part of the method of separation of variables). Perhaps what is needed is less of a focus on, say, what might appear on the equation sheet and more on the basic tenets of quantum mechanics.
RS
RS
Wednesday, April 23, 2008
Particle in a Finite Box and the Harmonic Oscillator
When we solved the system in which a particle is confined to an infinite box (that is, an infinite square well), we saw that quantum numbers arose naturally through the enforcement of continuity conditions (that th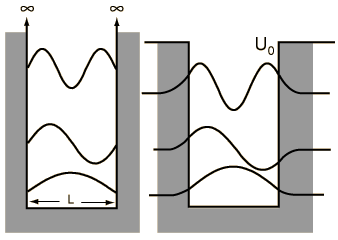 e wavefunction ψ must go to zero at x=0 and x=L). Quantization of energy and position (namely, nodes at which the particle cannot exist) are directly to these quantum numbers, whose values are n=1, 2, ..., ∞, representing an infinite number of energy levels.
e wavefunction ψ must go to zero at x=0 and x=L). Quantization of energy and position (namely, nodes at which the particle cannot exist) are directly to these quantum numbers, whose values are n=1, 2, ..., ∞, representing an infinite number of energy levels.
 e wavefunction ψ must go to zero at x=0 and x=L). Quantization of energy and position (namely, nodes at which the particle cannot exist) are directly to these quantum numbers, whose values are n=1, 2, ..., ∞, representing an infinite number of energy levels.
e wavefunction ψ must go to zero at x=0 and x=L). Quantization of energy and position (namely, nodes at which the particle cannot exist) are directly to these quantum numbers, whose values are n=1, 2, ..., ∞, representing an infinite number of energy levels.A particle in a finite box, however, can tunnel into the walls, in the same fashion that we saw earlier with the two barrier problems. Solving this system is not difficult but, unfortunately, has no analytical solution and must be solved either numerically or, as was done in class, graphically. On the other hand, the wavefunctions are essentially just those from the infinite box but are allowed to bleed into the wall (with the caveat that higher energy states tunnel further than the lower energy states). To summarize the major differences between the particle in a finite box and one in an infinite box:
- only a finite number of energy levels exist [called bound states]
- tunneling into the barrier is possible
- higher energy states are less tightly bound than lower states
- a particle given enough energy can break free [in other words, unbound]
One important distinction from the particle in a box result is that the peaks in the wavefunction are not uniform. For example, for v=2 and larger, it is clear that outside peaks (representing larger displacement from x=0) have higher probability than inside peaks. As n gets large, we see another clear example of the correspondence principle.
Thursday, April 17, 2008
Wednesday, April 16, 2008
Finite Barrier Tunneling and the Uncertainty Principle
 When a quantum particle encounters a discontinuity in the form of a finite barrier, there is a nonzero probability that it will be transmitted to the other side of the barrier. In fact, as the graphic at right shows, the wavefunction bifurcates into a reflected as well as a transmitted part, a decidedly nonclassical and headscratching result (remember the Copenhagen interpretation) -- the three curves, by the way, show the real and imaginary parts of the wavefunction as well as the probability density.
When a quantum particle encounters a discontinuity in the form of a finite barrier, there is a nonzero probability that it will be transmitted to the other side of the barrier. In fact, as the graphic at right shows, the wavefunction bifurcates into a reflected as well as a transmitted part, a decidedly nonclassical and headscratching result (remember the Copenhagen interpretation) -- the three curves, by the way, show the real and imaginary parts of the wavefunction as well as the probability density.Such tunneling phenomena are found throughout physics, chemistry and molecular biology, from explanations of alpha and beta decay to kinetic isotope effects and electron and proton transport in enzymes. It is likely that all redox chemistry has a tunneling component, which becomes even more prominent as the temperature falls.
Before moving onto the next quantum system, the particle in a finite box, we take a moment to consider one of the most important discoveries in all of quantum mechanics, the uncertainty principle. Heisenberg, in his development of matrix mechanics (an alternate description of quantum behavior, using matrices instead of differential operators), he discovered that some matrices did not commute, particularly those for momentum and position. After a little work he was able to demonstrate that this placed limits on the knowledge of the corresponding observable and we were doomed to indeterminacy. In particular, he found that ∆x∆p ≥ hbar/2, where ∆x and ∆p are the standard deviations of position and momentum.
Classically these values are zero: we can always know the position of, say, a marble and its velocity (and hence its momentum). At the quantum scale, these values are nonzero and, more baffling, are connected. The more precise we can nail down the position, for example, the less we will know about its momentum (and vice versa). Clearly we have to give up the Newtonian idea of knowing the trajectory of any quantum particle. This is not really an issue with measurement itself but rather a fundamental description of the quantum nature of the universe.
As we will see there are a number of uncertainty principles and they arise whenever we have noncommutative operators. In other words, whenever [a,b] ≠ 0, we will have an uncertainty principle in the corresponding observables: ∆a∆b ≥ hbar/2.
Solving the Schrödinger Equation
To understand simple quantum systems and solving the appropriate Schrödinger equation, we move through increasingly complicated systems. Whenever such an equation is solved, we typically acquire the wavefunction ψ and expressions for the energy E.
system I
A free particle in a potential of V=0. The general solution to the SE can be expressed two ways, both of which are commonly used: ψ = A'sin(kx) + B'cos(kx) or ψ = Aeikx+Be-ikx (the latter used when we care about which direction the particle is moving, the former when we want mathematical nicety). The wavevector k is equal to √2mE/h_bar.
system II
A particle in a potential of V=Vo. The general solutions are the same as in system I, except here k=√2mT/h_bar, where T is the kinetic energy. Since k = 2π/λ, we can see that the wavelength decreases as T increases.
system III
A particle confined to an infinite one-dimensional square well (V=0 inside). Here the wavefunctions are ψn=√2/L sin(nπx/L) and the energies are En=n2h2/8mL2 where n = 1, 2, ...
Three nonclassical results arise: (a) quantization of energy, which arises from putting constraints on the wavefunction (requiring it to go to zero at x=0 and x=L), (b) appearance of nodes, which limit positions at which a particle can exist in a box, and (c) nonzero ground-state (also known as the zero point energy). This "particle in a box" problem has been used to model, among other things, electrons in conjugated molecules and electrons in wires. Moreover it is one of the easier quantum systems to solve that simply demonstrates the important concepts of quantization of energy, nodes, normalization. and the correspondence principle.
system IV
A particle confined to a two-dimensional infinite box (V=0, ∞ outside). Using the method of separation of variables, we assume that ψ=X(x)Y(y), put it back into the SE and, while crossing our fingers, hope that it will crack into two equations. Fortunately it does just that, giving multiplicative wavefunctions ψ(x,y) = 2/√LxLy sin(nxπx/Lx)sin(nyπy/Ly) and additive energies E=h2/8m(nx2/Lx2 + ny2/Ly2). The solution clearly gives two quantum numbers (arising from two dimensions/coordinates) and the possibility of degeneracy arises, where two or more distinct wavefunctions have the same energy. The extension to three-dimensional boxes (or higher) should be straightforward to write down without solving the Schrödinger Equation from scratch.
system V
The barrier problem, in which a particle experiences a discontinuity in potential; for example, going from V=0 to V=Vo at x=0. Fortunately we know these solutions from systems I and II and can write them down immediately: ψI = Aeikx+Be-ikx and ψII = Ceikx+De-ikx. We note, however, since there is nothing to reflect the particle back once it passes the barrier, that D=0.
To make these wavefunctions plausible we must "glue" them together; in other words, we must make them connect [ψI(x=0)=ψII(x=0)] and connect smoothly [dψI/dx(x=0)=dψII/dx(x=0)].
When we calculate the transmission probability T=C*C/A*A, we find that it can never equal unity (meaning that there will always be some amount of reflection from a barrier. Also, when the particle energy E is less than the potential Vo we find that the particle can exist in the barrier to a finite, though exponentially decaying degree. Such penetration into the classical forbidden area is called tunneling, a very important phenomenon in quantum chemistry and the subject of the next lecture.
system I
A free particle in a potential of V=0. The general solution to the SE can be expressed two ways, both of which are commonly used: ψ = A'sin(kx) + B'cos(kx) or ψ = Aeikx+Be-ikx (the latter used when we care about which direction the particle is moving, the former when we want mathematical nicety). The wavevector k is equal to √2mE/h_bar.
system II
A particle in a potential of V=Vo. The general solutions are the same as in system I, except here k=√2mT/h_bar, where T is the kinetic energy. Since k = 2π/λ, we can see that the wavelength decreases as T increases.
system III
A particle confined to an infinite one-dimensional square well (V=0 inside). Here the wavefunctions are ψn=√2/L sin(nπx/L) and the energies are En=n2h2/8mL2 where n = 1, 2, ...
Three nonclassical results arise: (a) quantization of energy, which arises from putting constraints on the wavefunction (requiring it to go to zero at x=0 and x=L), (b) appearance of nodes, which limit positions at which a particle can exist in a box, and (c) nonzero ground-state (also known as the zero point energy). This "particle in a box" problem has been used to model, among other things, electrons in conjugated molecules and electrons in wires. Moreover it is one of the easier quantum systems to solve that simply demonstrates the important concepts of quantization of energy, nodes, normalization. and the correspondence principle.
system IV
A particle confined to a two-dimensional infinite box (V=0, ∞ outside). Using the method of separation of variables, we assume that ψ=X(x)Y(y), put it back into the SE and, while crossing our fingers, hope that it will crack into two equations. Fortunately it does just that, giving multiplicative wavefunctions ψ(x,y) = 2/√LxLy sin(nxπx/Lx)sin(nyπy/Ly) and additive energies E=h2/8m(nx2/Lx2 + ny2/Ly2). The solution clearly gives two quantum numbers (arising from two dimensions/coordinates) and the possibility of degeneracy arises, where two or more distinct wavefunctions have the same energy. The extension to three-dimensional boxes (or higher) should be straightforward to write down without solving the Schrödinger Equation from scratch.
system V
The barrier problem, in which a particle experiences a discontinuity in potential; for example, going from V=0 to V=Vo at x=0. Fortunately we know these solutions from systems I and II and can write them down immediately: ψI = Aeikx+Be-ikx and ψII = Ceikx+De-ikx. We note, however, since there is nothing to reflect the particle back once it passes the barrier, that D=0.
To make these wavefunctions plausible we must "glue" them together; in other words, we must make them connect [ψI(x=0)=ψII(x=0)] and connect smoothly [dψI/dx(x=0)=dψII/dx(x=0)].
When we calculate the transmission probability T=C*C/A*A, we find that it can never equal unity (meaning that there will always be some amount of reflection from a barrier. Also, when the particle energy E is less than the potential Vo we find that the particle can exist in the barrier to a finite, though exponentially decaying degree. Such penetration into the classical forbidden area is called tunneling, a very important phenomenon in quantum chemistry and the subject of the next lecture.
Tuesday, April 15, 2008
Extracting Information from a Wavefunction
In a given quantum system, the wavefunction ψ is said to contain all of the information knowable about that system; the only trick is getting it out and that is where operators come in. A fundamental postulate of quantum mechanics is that every measurable quantity, whether it is total energy, angular momentum, position, etc, has a corresponding quantum mechanical operator. The position and momentum operators are of particular importance since nearly all other relevant operators can be constructed from them.
Sometimes when an operator operates on a wavefunction we get, as a result, a constant multiplied by that wavefunction; in other words, an eigenvalue equation. When we obtain such an eigenvalue equation, the corresponding eigenvalue represents the only value for that observable. When we do not obtain an eigenvalue equation, our observables will not be singly-valued; in other words, the observable will span a range of values.
Although we hope for eigenvalue equations, we can still calculate values for observables, but we are doomed to talk only about probabilities. For example, when the position operator x doesn't give an eigenvalue, we can refer instead to the expectation value for x (represented by
Sometimes when an operator operates on a wavefunction we get, as a result, a constant multiplied by that wavefunction; in other words, an eigenvalue equation. When we obtain such an eigenvalue equation, the corresponding eigenvalue represents the only value for that observable. When we do not obtain an eigenvalue equation, our observables will not be singly-valued; in other words, the observable will span a range of values.
Although we hope for eigenvalue equations, we can still calculate values for observables, but we are doomed to talk only about probabilities. For example, when the position operator x doesn't give an eigenvalue, we can refer instead to the expectation value for x (represented by
Monday, April 7, 2008
Wave Mechanics and the Schrödinger Equation
 Two of the aforementioned failures of classical physics lead directly to the earthshaking matter-wave hypothesis of deBroglie: Einstein had demonstrated the wave-particle duality of light through his theory of the photon and Bohr, through his solar-system model of the hydrogen atom, hinted at the quantization of electron energies (we will cover his model more thoroughly when we get to atoms but the basics are well known to anyone who has taken general chemistry). Using a few equations from special relativity, deBroglie not only assumed that all matter had wavelike (as well as particle) properties, but in 1923 he derived a very simple relationship between wavelength and momentum: λ=h/p. In doing so, he essentially bridged what is now called the "old quantum theory", which lasted for about twenty years, to the much more successful (and abstract and perhaps unsettling) quantum mechanics of Schrödinger and Heisenberg.
Two of the aforementioned failures of classical physics lead directly to the earthshaking matter-wave hypothesis of deBroglie: Einstein had demonstrated the wave-particle duality of light through his theory of the photon and Bohr, through his solar-system model of the hydrogen atom, hinted at the quantization of electron energies (we will cover his model more thoroughly when we get to atoms but the basics are well known to anyone who has taken general chemistry). Using a few equations from special relativity, deBroglie not only assumed that all matter had wavelike (as well as particle) properties, but in 1923 he derived a very simple relationship between wavelength and momentum: λ=h/p. In doing so, he essentially bridged what is now called the "old quantum theory", which lasted for about twenty years, to the much more successful (and abstract and perhaps unsettling) quantum mechanics of Schrödinger and Heisenberg.The mathematical description of traveling and standing waves, utilizing terms like amplitude, frequency, wavelength, wavevector and period, had already been well-established by the mid-19th century. The Schrödinger Equation, though invoking these same mathematical constructs, can not be derived from any theory: it is simply asserted as a complete description of the physics of small particles. When the potential experienced by a particle of mass m is time-independent, we get the following equation (which should be committed to memory for any student studying quantum mechanics):
 What changes from problem to problem is the nature of the potential V and the coordinate system, which will change the form of the laplacian operator and what is obtained when the Schrodinger Equation is solved are mathematical descriptions of the wavefunction ψ and the energy E. We will soon see that ψ contains all the possible information about the quantum system but what is not so trivial is getting that information out. For that we will need the ideas of operator alebra and eigenvalue equations.
What changes from problem to problem is the nature of the potential V and the coordinate system, which will change the form of the laplacian operator and what is obtained when the Schrodinger Equation is solved are mathematical descriptions of the wavefunction ψ and the energy E. We will soon see that ψ contains all the possible information about the quantum system but what is not so trivial is getting that information out. For that we will need the ideas of operator alebra and eigenvalue equations.Next up: Descriptions of the momentum and position operators, followed by the very important hamiltonian operator, and our first solution to the Schrödinger Equation, the so-called particle in a box problem.
Friday, April 4, 2008
The Failures of Classical Physics
Quantum mechanics represents such a break from classical [Newtonian] mechanics and is still -- 100 years later -- so anti-intuitive, that we pause to look at three experiments/observations that demonstrated the cracks arising back then in classical physics: blackbody radiation, the photoelectric effect and atomic spectra.

At room temperature a blackbody [that is, a body which reflects no incident light] emits infrared light but, as it is heated, this radiation moves into the visible spectrum, beginning at orange and increasing towards bluish white. Using classical theories, Rayleigh and Jeans derived an equation for the spectral density (energy density per unit frequency per volume) as a function of frequency. This model, however, was a horrible failure in that it did not correlate at all with experimental results, leading instead to a spectral density that reaches infinity in the ultraviolet regime [leading to what we now call the ultraviolet catastrophe].
Max Planck, in 1900, solved the problem (and unwittingly triggered the quantum revolution) by assuming that the blackbody was made of oscillators that could emit energy only in packets of nhν, where n is a nonnegative integer and h is a constant (now called Planck's constant). This assumption leads directly to the Planck distribution, which fit the experimental data perfectly when h=6.626E-34 Js. He spent the next few years unconvinced that h had much physical meaning and was not a strong supporter of the quantum theory, but by the time Einstein and Bohr hopped aboard, the train had left the station.
The photoelectric effect, in which light shined onto a metal induces a current [but only if its frequency is above some threshold], was also a mystery awaiting an explanation. Einstein's radical 1905 postulate, for which he won the Nobel Prize in Physics, was that light was comprised of corpuscular [particle-like] packets of energy hν called photons. The photoelectric effect could then be understood as a simple collision between two particles -- the photon and the electron in the metal. If the frequency of light were high enough, it would have an energy sufficient to overcome the binding energy [called the work function] of the electron to the metal. Einstein also, to his chagrin years later, the idea of the wave-particle duality, which is one of the more fundamental and vexing aspects of quantum mechanics.
When the emitted light of a heated gas is separated through a prism, a line spectrum occurs [as opposed to the continuous rainbow-type spectrum seen from sunlight]. The wavelengths of these lines could be fit to the Rydberg formula but, since it is simply an empirical formula and not based on any underlying theory, it further demonstrated the problems of classical physics. The Rydberg formula was eventually theoretically derived in the work of Bohr, whose model of the hydrogen atom we will visit a little later.
Much of what we have described thus far, including the early work of Planck, Einstein and Bohr, is generally referred to as the old quantum theory. One giant step further, spurred on by the work of deBroglie, is quantum mechanics, which we will visit next.

At room temperature a blackbody [that is, a body which reflects no incident light] emits infrared light but, as it is heated, this radiation moves into the visible spectrum, beginning at orange and increasing towards bluish white. Using classical theories, Rayleigh and Jeans derived an equation for the spectral density (energy density per unit frequency per volume) as a function of frequency. This model, however, was a horrible failure in that it did not correlate at all with experimental results, leading instead to a spectral density that reaches infinity in the ultraviolet regime [leading to what we now call the ultraviolet catastrophe].
Max Planck, in 1900, solved the problem (and unwittingly triggered the quantum revolution) by assuming that the blackbody was made of oscillators that could emit energy only in packets of nhν, where n is a nonnegative integer and h is a constant (now called Planck's constant). This assumption leads directly to the Planck distribution, which fit the experimental data perfectly when h=6.626E-34 Js. He spent the next few years unconvinced that h had much physical meaning and was not a strong supporter of the quantum theory, but by the time Einstein and Bohr hopped aboard, the train had left the station.
The photoelectric effect, in which light shined onto a metal induces a current [but only if its frequency is above some threshold], was also a mystery awaiting an explanation. Einstein's radical 1905 postulate, for which he won the Nobel Prize in Physics, was that light was comprised of corpuscular [particle-like] packets of energy hν called photons. The photoelectric effect could then be understood as a simple collision between two particles -- the photon and the electron in the metal. If the frequency of light were high enough, it would have an energy sufficient to overcome the binding energy [called the work function] of the electron to the metal. Einstein also, to his chagrin years later, the idea of the wave-particle duality, which is one of the more fundamental and vexing aspects of quantum mechanics.
When the emitted light of a heated gas is separated through a prism, a line spectrum occurs [as opposed to the continuous rainbow-type spectrum seen from sunlight]. The wavelengths of these lines could be fit to the Rydberg formula but, since it is simply an empirical formula and not based on any underlying theory, it further demonstrated the problems of classical physics. The Rydberg formula was eventually theoretically derived in the work of Bohr, whose model of the hydrogen atom we will visit a little later.
Much of what we have described thus far, including the early work of Planck, Einstein and Bohr, is generally referred to as the old quantum theory. One giant step further, spurred on by the work of deBroglie, is quantum mechanics, which we will visit next.
Subscribe to:
Posts (Atom)


